Modeling and Optimization of Thermal Energy Storage Systems
Energy can be stored in many different forms. Thermal energy storage (TES) is stored energy in the form of heat or cooling. Because of the simplicity of storing thermal energy, TES is very cost-effective, as long as it is utilized correctly. Chilled water TES systems can be used in large buildings or in district energy systems with centralized cooling to shift the system’s electricity demand profile. Cooling can be done in off-peak hours, like at night, so that the peak demand can be shaved in the hot afternoon, when energy prices tend to peak. Hot TES can be used in colder climates, where solar energy can be stored during the day and used for heating at night. TES is absolutely essential in concentrated solar power systems, allowing these systems to produce uninterrupted power despite intermittent cloud cover.
A particularly effective method for storing thermal energy is in a thermocline tank, where the hot fluid and cold fluid are separated from each other using differences in density of the hot and cold fluid.
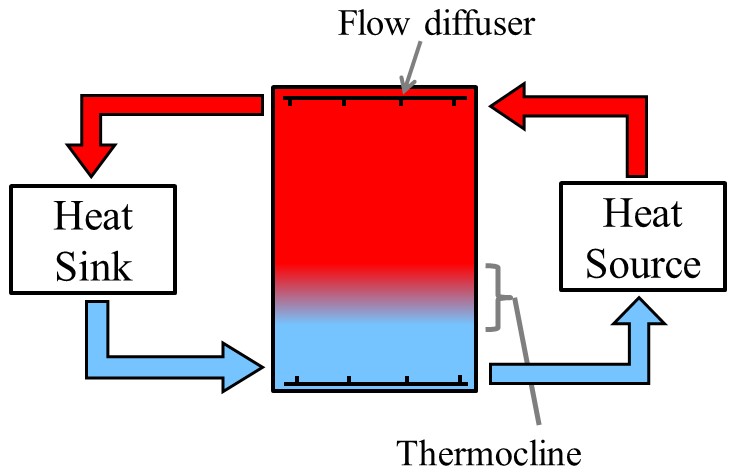
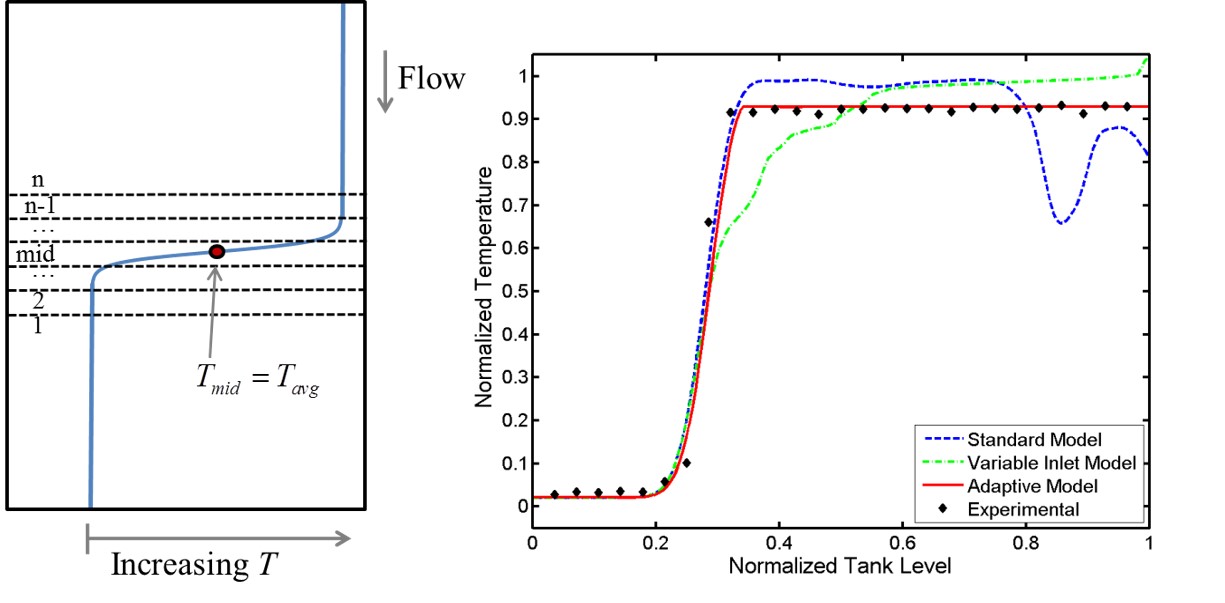
My collaborators and I have developed a novel method for dynamic modeling of thermocline TES systems. We use an adaptive method, where the nodes used to model the stratified region of the tank move with the temperature profile. ,This method is much more computationally efficient (and surprisingly more accurate) than traditional modeling techniques.
Read more here
An adaptive-grid model for dynamic simulation of thermocline energy storage systems
Optimal chiller loading in a district cooling system with thermal energy storage
Optimization and advanced control of thermal energy storage systems
Model Predictive Control for Photovoltaic Systems with Batteries
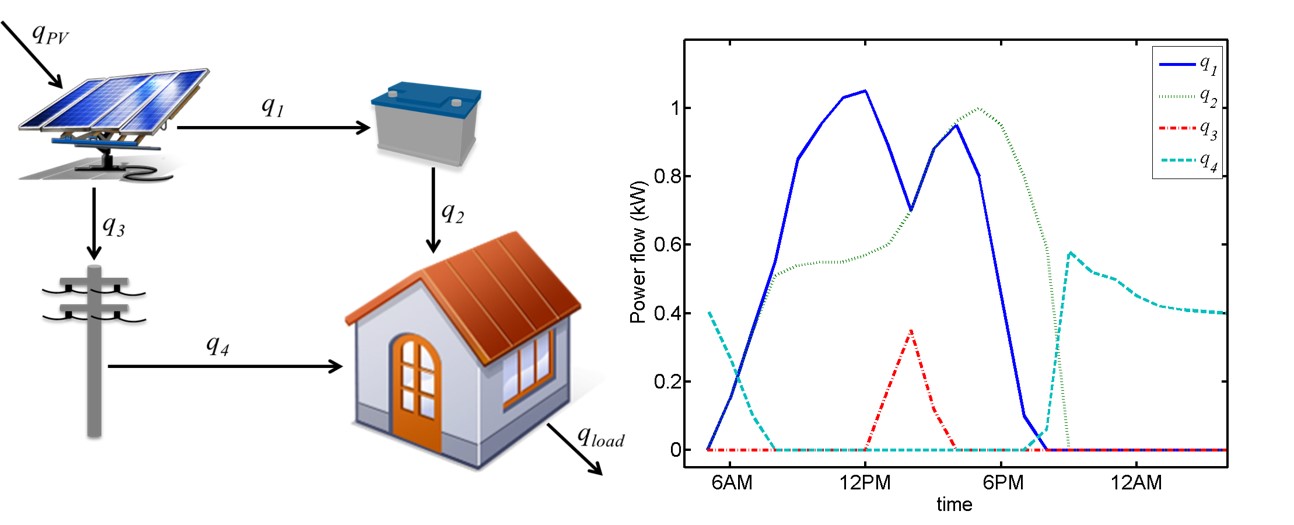
While thermal systems can use thermal energy storage, electric systems require battery storage. When integrated with photovoltaics, battery storage gives the user more flexibility concerning how (or more precisely, when) their solar power is used. We’ve developed a novel methodology for representing discrete decisions (such as switching power flow) into a purely continuous model, which can be solved very quickly for use in model predictive control.
Read more here
Nonlinear modeling, estimation, and predictive control in APMonitor
